Физика - Молекулярные колебания

Молекулярные колебания один из трёх типов молекулярного движения, к которым относятся также

трансляционное движение (когда все атомы молекулы смещаются в одном направлении) и

вращательное движение (когда молекула поворачивается на определённый угол). В отличие от

последних двух случаев, когда геометрия молекулы не меняется, при колебаниях происходит

изменение положения атомов относительно друг друга.

В общем случае, молекула из N атомов обладает 3N — 6 нормальными колебаниями, за

исключением линейных молекул, у которых 3N — 5 колебаний. Двухатомная молекула,

как частный случай линейной, обладает всего одним колебанием, при котором меняется

расстояние между двумя атомами молекулы.

Типы колебаний

В случае многоатомных молекул колебания довольно сложны и их обычно описывают как комбинацию

колебаний разных фрагментов молекулы. Часто это трёхатомные фрагменты молекулы, например

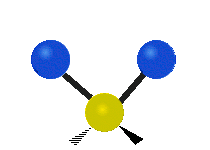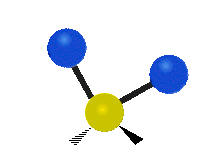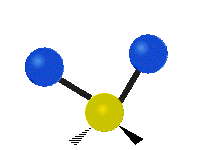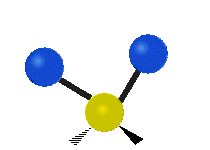
метиленовая группа (-CH₂-) в органических молекулах. Можно выделить шесть типов колебаний

трёхатомного фрагмента молекулы: симметричное и антисимметричное валентные колебания,

ножничное, маятниковое, веерное и крутильное. Следует отметить, что для молекул содержащих

только три атома, например молекулы воды, последние три типа колебаний не существуют, так как в

данном случае они соответствуют просто вращениям молекулы относительно трёх

взаимно перпендикулярных осей (для этих колебаний расстояния между тремя атомами фрагмента не

меняются).

Валентные колебания (Stretching)		Ножничное (Scissoring)
Симметричное	Антисимметричное	Ножничное (Scissoring)

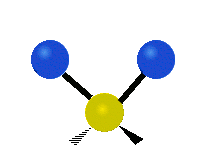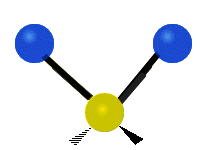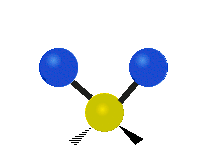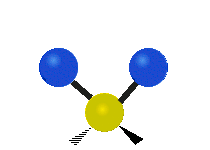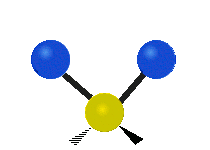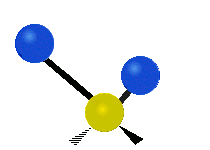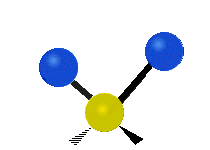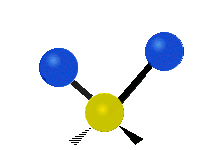Маятниковое (Rocking)	Веерное (Wagging)	Крутильное (Twisting)

Энергия колебаний

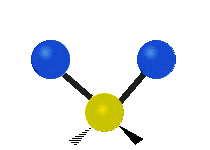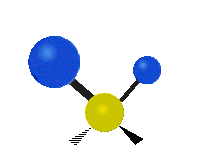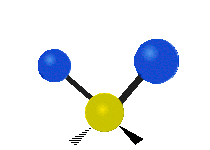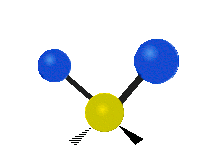Классическая механика

ведут себя как пружины. В гармоническом приближении колебания подчиняются закону Гука: Сила $F$ ,

В классической механике колебания молекулы рассматриваются с позиции, что связи между атомами

которую требуется приложить для растяжения пружины, прямо пропорциональна величине

растяжения $Q$ . Константа пропорциональности в случае молекулярных колебаний называется

силовой константой, $k$ .

${\mathrm {F}}=-kQ\!$

Из Второго закона Ньютона эта сила равняется также произведению приведённой массы $\mu$ и ускорения:

${\mathrm {F}}=\mu {\frac {d^{2}Q}{dt^{2}}}$

Из этого получаем обыкновенное дифференциальное уравнение:

$\mu {\frac {d^{2}Q}{dt^{2}}}+kQ=0$

Решением которого являются гармонические колебания:

$Q(t)=A\cos(2\pi \nu t);\ \ \nu ={1 \over {2\pi }}{\sqrt {k \over \mu }}.\!$

где $A$ — амплитуда координаты колебания $Q$ . Для двухатомной молекулы AB приведённая

масса $\mu$ равняется:

${\frac {1}{\mu }}={\frac {1}{m_{A}}}+{\frac {1}{m_{B}}}$ , где m_A и m_B — массы атомов A и B.

В гармоническом приближении потенциальная энергия молекулы $V$ является квадратичной

функцией от нормальной координаты. В этом случае силовая константа равна второй производной

потенциальной энергии:

$k={\frac {\partial ^{2}V}{\partial Q^{2}}}$

Квантовая механика

В квантовой механике, также как и в классической, потенциальная энергия гармонического

осциллятора является квадратичной функцией от нормальной координаты. Из решения уравнения

Шрёдингера возможны следующие значения энергии колебаний:

$E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!$ ,

где n — квантовое число, которое принимает значения 0, 1, 2 ... В молекулярной спектроскопии это

колебательное квантовое число часто обозначается как v, так как возможны и другие типы энергии

молекулы, которым соответствуют другие квантовые числа.

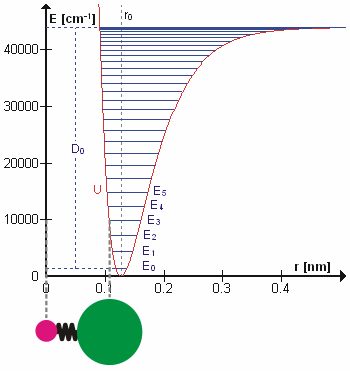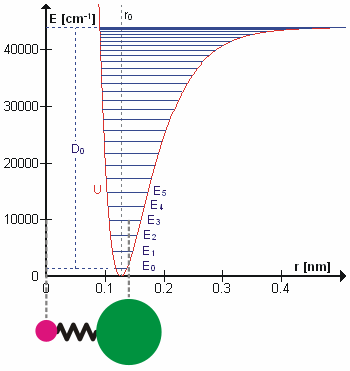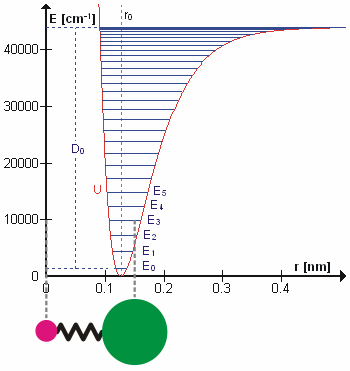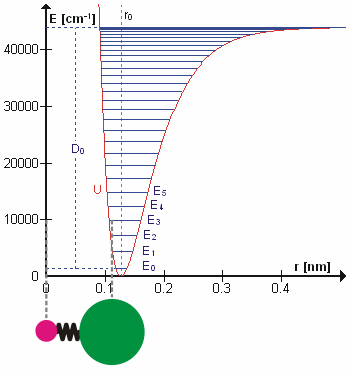
Молекула HCl как пример ангармонического осциллятора колеблющегося с энергией E₃. D₀ — энергия диссоциации

, r₀ —длина связи, U — потенциальная энергия. Энергия выражена вволновых числах.

Информация взята с сайта ru.wikipedia.org