Квантовая оптика

В соответствии с основными положениями квантовой теории Планка и Эйнштейна, излучение, и, в частности, видимый свет обладает корпускулярными свойствами. Очевидно, что при определенных условиях эти свойства должны проявляться в оптических экспериментах.

      Класс оптических явлений, для объяснения которых следует привлекать представления о квантах энергии излучения и их носителях - фотонах, получил название явлений квантовой оптики. Такие явления связаны, прежде всего, с взаимодействием излучения с веществом, которое удается описать как взаимодействие частиц излучения (фотонов) с частицами вещества. Рассмотрим два таких явления квантовой оптики.

     Фотоэффект. Определим внешний фотоэффект как явление испускания электронов вещества под действием излучения. Впервые фотоэффект был открыт в 1887 г. Г.Герцем, который обнаружил, что искровой разряд между двумя металлическими шариками происходит значительно интенсивнее, если один из шариков освещать ультрафиолетовыми лучами. Измерение удельного заряда вылетающих из металла под действием излучения частиц позволило установить, что частицы являются электронами.

      Хотя эмиссия электронов под действием излучения наблюдается практически для всех веществ, наиболее часто фотоэффект связывают с металлами, в которых существуют оторванные от атомов "свободные" электроны, удерживаемые внутри металла некоторым энергетическим барьером вблизи его поверхности. Преодолевая этот барьер при вылете из металла, электрон совершает работу выхода, затрачивая на это часть своей кинетической энергии. Работа выхода  электронов из металлов составляет порядка нескольких электрон-вольт.

      Детальное экспериментальное исследование закономерностей внешнего фотоэффекта для металлов было выполнено в 1888 г. А.Г.Столетовым на установке с фотоэлементом, схема которой приведена на рис. 1.12. Фотоэлемент в виде вакуумной двухэлектродной лампы имеет металлический катод К, который при освещении его через кварцевое окошко видимым светом или ультрафиолетовым излучением испускает электроны. Вылетевшие из катода фотоэлектроны, достигая анода А, обеспечивают протекание в цепи электрического тока, который фиксируется гальванометром или миллиамперметром. Специальная схема подключения источника позволяет изменять полярность напряжения, подаваемого на фотоэлемент.

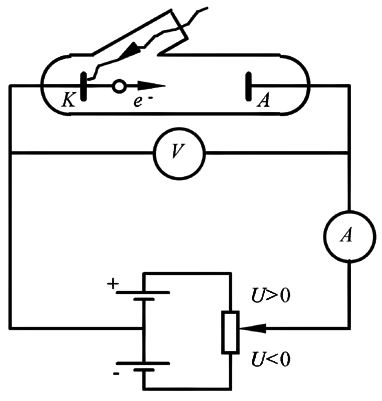Рис. 1.12.

      Качественный вид вольт-амперной характеристики такого фотоэлемента, то есть зависимости фототока  от напряжения  между катодом и анодом для случая неизменного светового потока, падающего на катод, представлена на рис. 1.13.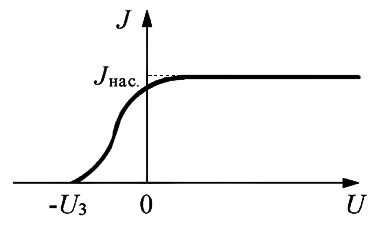

Рис. 1.13.

      Положительное напряжение соответствует ускоряющему электрическому полю, в которое попадают вылетающие из катода электроны. Поэтому, в области положительных напряжений все испускаемые катодом электроны достигают анода, обуславливая фототок насыщения .

      Небольшой спад фототока при малых положительных напряжениях, который наблюдается в опытах, связан с контактной разностью потенциалов между катодом и анодом. Ниже, при обсуждении закономерностей фотоэффекта мы будем пренебрегать влиянием контактной разности потенциалов.

      При отрицательном напряжении  испущенный катодом электрон попадает в тормозящее электрическое поле, преодолеть которое он может лишь имея определенный запас кинетической энергии. Электрон с малой кинетической энергией, вылетев из катода, не может преодолеть тормозящее поле и попасть на анод. Такой электрон возвращается на катод, не давая вклада в фототок. Поэтому, плавный спад фототока в области отрицательных напряжений указывает на то, что вылетающие из катода фотоэлектроны имеют разные значения кинетической энергии.

      При некотором отрицательном напряжении, величину которого  называют задерживающим напряжением (потенциалом), фототок становится равным нулю. Соответствующее тормозящее электрическое поле при этом задерживает все вылетающие из катода электроны, включая электроны с максимальной кинетической энергией .

      Измерив задерживающее напряжение, можно определить эту максимальную энергию или максимальную скорость  фотоэлектронов из соотношения

     

.

(1.54)

      Экспериментально были установлены следующие основные закономерности фотоэффекта:

     Для монохроматического света определенной длины волны фототок насыщения пропорционален световому потоку, падающему на катод.

     Максимальная кинетическая энергия фотоэлектронов не зависит от величины светового потока, а определяется лишь частотой излучения.

     Для каждого вещества катода существует своя граничная частота  такая, что излучение с частотой  фотоэффекта не вызывает. Эту граничную частоту называют частотой красной границы фотоэффекта. По шкале длин волн ей соответствует длина волны красной границы , такая, что фотоэффект из данного металла вызывает излучение лишь с меньшей длиной волны .

      Попытки объяснить закономерности фотоэффекта с использованием классической волновой теории, в которой излучение рассматривалось как электромагнитные волны, приводили к выводам, противоположным наблюдаемым в эксперименте. Действительно, объясняя вырывание электронов из металла силовым воздействием на них со стороны электрического поля волны, такая теория неизбежно приходила к выводу о том, что максимальная кинетическая энергия фотоэлектронов должна определяться световым потоком, падающим на катод. Наличие красной границы у фотоэффекта также противоречило выводам волновой теории.

      Именно для объяснения экспериментов по фотоэффекту в 1905 г. Эйнштейн предложил концепцию фотонов как частиц излучения, несущих квант энергии. Рассмотрев в такой теории процесс взаимодействия излучения с металлом как процесс неупругого соударения фотона со свободным электроном металла, Эйнштейн легко объяснил закономерности фотоэффекта. Действительно, в таком процессе электрон приобретает всю энергию от фотона, которая пропорциональна частоте излучения. Число же вырванных из металла электронов и, тем самым, фототок насыщения, пропорционально числу падающих на металл фотонов, которое определяется величиной потока энергии излучения.

      Если в такой модели процесса пренебречь потерями энергии электрона при его движении внутри металла по направлению к поверхности, то закон сохранения энергии приводит к соотношению

     

,

(1.55)

     которое называют уравнением Эйнштейна для внешнего фотоэффекта. Здесь  - максимальная энергия фотоэлектронов.

      Непосредственным следствием этого уравнения являются второй и третий законы фотоэффекта. Действительно, из (1.55) следует, что максимальная энергия фотоэлектронов зависит от частоты падающего на металл излучения. Кроме того, если , то фотоэффект не должен наблюдаться. Отсюда, для частоты и длины волны красной границы фотоэффекта получаем простые формулы

     

,

(1.56)

     из которых следует, что эти характеристики полностью определяются значением работы выхода электрона из металла.

      Таким образом квантовая теория излучения, в отличие от волновой теории, достигает успеха в объяснении фотоэффекта. Единственным возражением к квантовому объяснению фотоэффекта мог бы выступить известный (см. задачу 1.7) вывод теории о том, что свободный электрон не может поглотить фотон, так как такой процесс запрещен законами сохранения энергии и импульса. Это возражение, однако, снимается, если учесть, что в металле электрон взаимодействует с атомами кристаллической решетки. Поэтому при поглощении электроном фотона часть импульса фотона может быть передана кристаллической решетке металла.

      В пользу квантовой природы фотоэффекта указывают также и выводы опытов Э.Майера и В.Герлаха, которые в 1914 г. исследовали фотоэлектрический эффект на мельчайших частицах металлической пыли. В этих опытах удалось оценить время, за которое частица приобретает энергию от излучения, достаточную для эмиссии электрона. Это время оказалось значительно меньше времени порядка нескольких секунд, которое должно было пройти для накопления энергии пылинкой, если считать, что энергия накапливается за счет поглощения электромагнитной волны.

      Важной количественной характеристикой фотоэффекта является квантовый выход , определяющий число вылетевших электронов, приходящихся на один падающий на металл фотон. Вблизи красной границы для большинства металлов квантовый выход составляет порядка 10^-4 электрон/фотон. Малость квантового выхода обусловлена тем, что энергию, достаточную для выхода из металла сохраняют только те электроны, которые получили энергию от фотонов на глубине от поверхности, не превышающей 0,1 мкм. Кроме того, поверхность металлов сильно отражает излучение. С увеличением энергии фотонов, то есть с уменьшением длины волны излучения квантовый выход увеличивается, составляя электрон/фотон для энергии фотонов порядка одного электрон-вольта. Для рентгеновского излучения с энергией фотонов эВ уже практически на каждые десять падающих на поверхность фотонов приходится один вылетевший из металла электрон.

      Фотоэффект нашел широкое применение в науке и технике. Так, записав уравнение Эйнштейна (1.55) в виде

     

,

(1.57)

     можно заметить, что график зависимости задерживающего напряжения от частоты излучения должен иметь вид прямой линии, наклон которой определяется значением постоянной Планка. Измерив этот наклон экспериментально для натрия, магния, меди и алюминия, Р.Милликен в 1914 г. с хорошей точностью вычислил значение постоянной Планка. В 1923 г. за работы в области элементарных зарядов и фотоэлектрического эффекта Милликен был удостоен Нобелевской премии по физике.

      Приборы, в основе устройства которых лежит фотоэффект, называют фотоэлементами. Обычный вакуумный фотоэлемент представляет собой вакуумированную колбу, внутреннюю поверхность которой, за исключением небольшого окошечка для доступа света, покрывает тонкая пленка из металла с малой работой выхода (цезий, калий, натрий). Анод представляет собой проволочное кольцо в центре колбы. Между катодом и анодом прикладывается ускоряющее напряжение порядка В. Фотоэлементы находят широкое применение в технике (фотореле, люксметры, системы звукозаписи на пленку и др.). В последнее время конкурентом вакуумных фотоэлементов стали фоторезисторы, в основе работы которых лежит внутренний фотоэффект в полупроводниках.

      Внешний фотоэффект используется также в фотоэлектронных умножителях (ФЭУ) - современных электронных приборах для регистрации и преобразования слабых световых сигналов. Такие приборы широко применяются в астрономии, прикладной оптике, ядерной физике. В ФЭУ фотоэлектронная эмиссия сочетается с системой умножения количества электронов, действие которой основано на явлении вторичной электронной эмиссии.

     Эффект Комптона. При большой энергии фотонов, в частности, для рентгеновского излучения ( МэВ) процесс поглощения фотонов электронами вещества становится маловероятным. В этом случае при взаимодействии электромагнитного излучения с веществом наблюдается его рассеяние с изменением направления распространения.

      В 1923 г. А.Комптон, изучая рассеяние рентгеновского излучения на парафине, обнаружил, что длина волны рассеянного излучения  больше, чем длина волны падающего излучения . Такой эффект увеличения длины волны излучения вследствие рассеяния его веществом получил название эффекта Комптона. Открытие и объяснение этого эффекта квантовой оптики в 1927 г. было удостоено Нобелевской премии по физике.

      Схематически экспериментальная установка Комптона изображена на рис. 1.14. Рентгеновская трубка РТ была смонтирована на вращающейся платформе, что позволяло при ее повороте изменять угол рассеяния  рентгеновского излучения, попадающего после мишени-рассеивателя М в измерительный блок установки.

Рис. 1.14.

      Длина волны рассеянного излучения определялась с помощью дифракции его на кристалле. Согласно дифракционной теории при выполнении условия Вульфа-Брегга

     

(1.58)

     где  - расстояние между атомными плоскостями кристалла, а  - угол скольжения падающего излучения, наблюдается интенсивное отражение от кристалла рассеянного рентгеновского излучения. Поэтому, зная параметры кристаллической решетки  и измерив угол  для максимума отражения -ого порядка, можно рассчитывать длину волны  рентгеновского излучения, рассеянного мишенью М. Соответствие угла  и длины волны , вытекающее из (1.58), позволяло нанести на фотопленке Ф шкалу длин волн и по положению на фотопленке засвеченной полоски определять длину волны рассеянного рентгеновского излучения. В первых опытах Комптона вместо фотопленки использовалась подвижная ионизационная камера, позволяющая по току в приборе фиксировать отраженное от кристалла рентгеновское излучение.

      Как установил экспериментально Комптон, длина волны рассеянного излучения оказалась больше длины волны падающего излучения, причем изменение длины волны не зависело от материала рассеивателя, а определялось только величиной угла рассеяния . Опытным путем Комптон показал, что

     

.

(1.59)

     Это соотношение называют формулой Комптона. Значение постоянной  м Комптон определил экспериментально.

      Увеличение длины волны излучения при его рассеянии необъяснимо с точки зрения волновой теории электромагнитного излучения. Как показал Дж.Томсон, в классической теории рассеяние можно рассматривать как процесс, в котором электрон совершает вынужденные колебания под действием электрического поля падающей волны. При этом электрон сам как антенна начинает излучать вторичные (рассеянные) сферические электромагнитные волны на частоте падающего излучения.

      Таким образом, эффект Комптона относится к явлениям квантовой оптики, и фотонная теория излучения объясняет этот эффект как следствие упругого рассеяния фотона на свободном электроне вещества (рис. 1.15). Формула Комптона (1.59) при этом оказывается следствием законов сохранения энергии и импульса в упругом соударении фотона и электрона.

      Действительно, в системе отсчета, в которой свободный электрон первоначально покоился, закон сохранения энергии с учетом возможных релятивистских скоростей электрона после удара может быть записан в виде

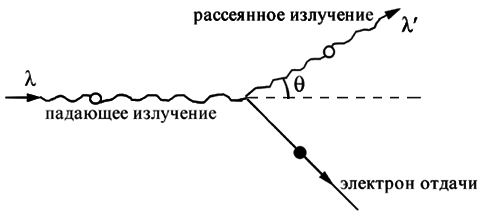Рис. 1.15.

     

.

(1.60)

     Здесь  - масса покоя электрона,  - масса движущегося электрона, который называют электроном отдачи,  - релятивистский множитель, а  - скорость электрона после столкновения с фотоном.

      Заметим, что уже закон сохранения энергии (1.60) объясняет эффект Комптона качественно. Действительно, так как , то из (1.60) следует, что .

      В упругом столкновении фотона с электроном выполняется также закон сохранения импульса, который с учетом (1.44) можно записать в виде

     

.

(1.61)

     Здесь , , а  - угол рассеяния.

      Построив векторную диаграмму закона сохранения импульса (рис. 1.16), из треугольника импульсов находим, что

     

     или

Рис. 1.16.

     

.

(1.62)

     Преобразовав (1.60) к виду

     

     и возведя это равенство в квадрат, получим

     

.

(1.63)

     Учитывая, что , запишем (1.63) в виде

     

.

(1.64)

     Следствием законов сохранения энергии и импульса в рассматриваемом процессе упругого столкновения фотона излучения со свободным электроном вещества является соотношение, которое следует из (1.62) и (1.64):

     

.

(1.65)

     Из (1.65) получаем формулу Комптона

     

.

(1.66)

     Величину  называют комптоновской длиной волны частицы, масса покоя которой равна . В нашем случае м - комптоновская длина волны электрона.

      Сравнение (1.66) с (1.59) показывает прекрасное совпадение выводов квантовой теории излучения и эксперимента. Из этих формул следует, что максимальное изменение длины волны излучения наблюдается для угла рассеяния , и оно равно . В силу малости значения  практически изменение длины волны при рассеянии на свободных электронах можно обнаружить лишь в экспериментах с коротковолновыми рентгеновским или гамма излучениями.

      Следует заметить, что значительная часть электронов вещества не является свободными, а связаны с атомами. Если энергия кванта излучения велика по сравнению с энергией связи электрона, то рассеяние на таком электроне происходит как на свободном электроне. В противном случае, рассеиваясь на связанном электроне, фотон обменивается энергией и импульсом фактически со всем атомом в целом. При таком рассеянии для расчета изменения длины волны излучения также можно применить формулу (1.66), где, однако, под  следует понимать уже массу всего атома. Это изменение оказывается настолько малым, что его нельзя практически обнаружить экспериментально.

      В реальных опытах по рассеянию излучения веществом часть электронов ведет себя как свободные, а часть - как связанные. Поэтому в рассеянном излучении наблюдается как смещенная (комптоновская) линия, так и несмещенная (томсоновская) линия. С увеличением атомного номера рассеивателя относительная доля связанных электронов увеличивается, что приводит к падению интенсивности комптоновской компоненты в спектре рассеянного излучения и к росту интенсивности томсоновской компоненты.

      В диапазоне энергий квантов  Мэ