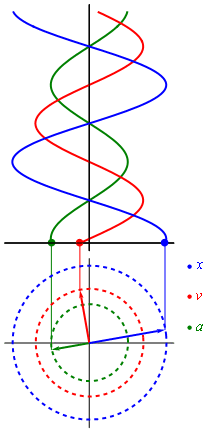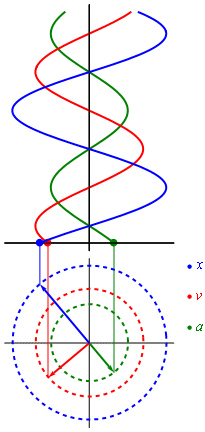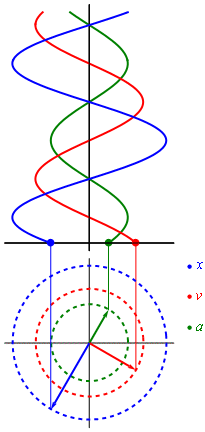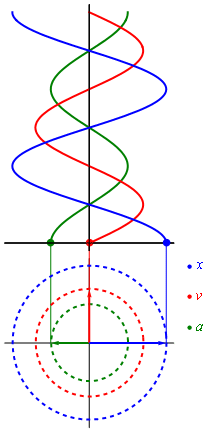
Физика - Гармонические колебания

Гармонические колебания — колебания, при которых физическая (или любая другая)

величина изменяется с течением времени по синусоидальному или косинусоидальному закону.

Кинематическое уравнение гармонических колебаний имеет вид.

Гармоническими являются колебания, которые происходят под действием силы, пропорциональной

смещению колеблющейся точки и направленной противоположно этому смещению.

$x(t)=A\sin(\omega t+\varphi )$

или

$x(t)=A\cos(\omega t+\varphi )$ ,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени

t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение

колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая

число полных колебаний происходящих в течение 2π секунд; $(\omega t+\varphi )$ — полная фаза колебаний,

$\varphi$ — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

${\frac {d^{2}x}{dt^{2}}}+\omega ^{2}x=0.$

(Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание

с циклической частотой $\omega .$ )

Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости.

Виды колебаний

Применение Свободные колебания совершаются под действием внутренних сил системы после

того, как система была выведена из положения равновесия. Чтобы свободные колебания были

гармоническими,необходимо, чтобы колебательная система была линейной (описывалась линейными

уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание

Вынужденные колебания совершаются под воздействием внешней периодической силы.

Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной
(описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем

как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:

Очень часто малые колебания, как свободные,так и вынужденные, которые происходят в реальных

системах, можно считать имеющими форму гармонических колебаний или очень близкую к ней.

Широкий класс периодических функций может быть разложен на сумму тригонометрических

компонентов. Другими словами, любое колебание может быть представлено как сумма гармонических

колебаний.

Для широкого класса систем откликом на гармоническое воздействие является гармоническое

колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой

характеристикой системы. С учётом предыдущего свойства это позволяет исследовать

прохождение колебаний произвольной формы через системы.

Эволюция во времени перемещения, скорости и ускорения при гармоническом движении

Информация взята с сайта ru.wikipedia.org