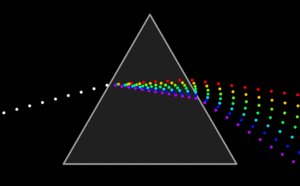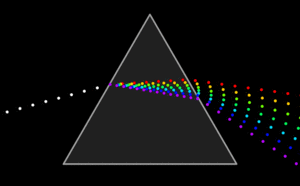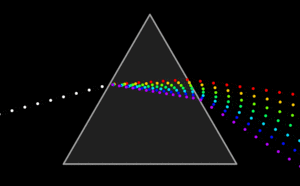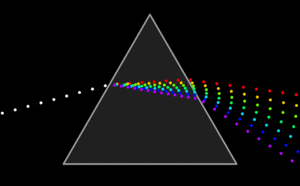
Геометрическая оптика
Геометрическая оптика или оптика луча, описывает распространение света термином луч. Работы Гюйгенса «Волновая теория света», которые были написаны под влиянием фундаментальных работ Ньютона, и вошли потом в «Оптику», оказали большое влияние на современников. Действительно, будучи приверженцем теории цветов Гука, он после работ Ньютона, восхищаясь их экспериментальной стороной, но не разделяя его теоретической интерпретации, пришёл к выводу, что «явление окрашивания остаётся ещё весьма таинственным из-за трудности объяснения этого разнообразия цветов с помощью какого-либо физического механизма». Поэтому он счёл наиболее целесообразным вообще не рассматривать вопроса о цветах в своём трактате.
В своем небольшом трактате первым он рассмотрел прямолинейное распространение света, во второй части — отражение, в третьей — преломление, в четвёртой — атмосферную рефракцию, в пятой — двойное лучепреломление и в шестой — формы линз.
Неудовлетворительное объяснение прямолинейного распространения света Гюйгенс возместил блестящим объяснением с помощью своего механизма частичного отражения, преломления и полного внутреннего отражения — явлений, интерпретация которых вынудила Ньютона усложнять свою теорию, нагромождая одну теорию на другую. По существу, эти объяснения Гюйгенса и сейчас приводятся во всех учебниках. Новая теория обладала также тем преимуществом, что для объяснения преломления она в соответствии со здравым смыслом требовала меньшей скорости в более плотной среде.
«Луч» в геометрической оптике — абстрактный геометрический объект, перпендикулярный фронту импульса фактических оптических волн. Геометрическая оптика описывает правила прохождения лучей через оптическую систему.
Приняв это абстрактное понятие и связанные с ним правила, мы существенно упрощаем задачу оптики, но не в состоянии объяснить много важных оптических эффектов, например дифракцию и поляризацию.
Параксиальное приближение
Следующее упрощение в геометрической оптике — параксиальное приближение, или «приближение малых углов». Математически поведение луча становится линейным, позволяя представить оптические компоненты простыми матрицами. Применение методов Гауссовской оптики позволяет найти свойства первого порядка оптических систем.
Гауссовское распространение луча — расширение параксиальной оптики, описывающее более точную модель поведения лучей. Используя параксиальное приближение и явление дифракции, данный набор методов описывает расширение светового пучка с расстоянием и минимальный размер светового пятна, в которое может быть сосредоточен световой пучок. Тем самым эта модель является промежуточной между геометрической и физической оптикой.
Физическая оптика
Физическая оптика или оптика волны основывается на принципе Гюйгенса и моделирует распространение сложных фронтов импульса через оптические системы, включая иамплитуду и фазу волны. Этот раздел оптики объясняет дифракцию, интерференцию, эффекты поляризации, аберрацию и природу других сложных эффектов.
В этом разделе оптики также используются приближения, а не полная электромагнитная модель распространения света. Однако в простых случаях, а по мере роста доступных вычислительных мощностей и в более сложных, становится возможным полный расчёт по точной теории.
Современная оптика
Современная оптика охватывает области оптической науки и разработок, которые стали популярными в XX столетии. Эти области оптической науки в основном касаются электромагнитных или квантовых свойств света, но включают и другие области.
Физиологическая оптика
Физиологическая оптика — междисциплинарная наука о зрительном восприятии света. Она объединяет сведения по биофизике, биохимии и психологии зрительного восприятия.
Рентгеновская оптика
Рентгеновская оптика — отрасль прикладной оптики, изучающая процессы распространения рентгеновских лучей в средах, а также разрабатывающая элементы для рентгеновских приборов. Рентгеновская оптика в отличие от обычной рассматривает электромагнитные волны в диапазоне длин волн рентгеновского 10−4 до 100 Å (от 10−14 до 10−8 м) и гамма-излучений < 10−4 Å.
Оптика геометрическая (формулы)
Скорость света в среде

Длина волны в среде

Предельный угол полного внутреннего отражения

Формула тонкой линзы

Увеличение линзы

Линейное поперечное увеличение

Если β < 0: 

Если β < 0: 
Оптическая сила линзы через координаты центров кривизны

Увеличение оптического прибора

Увеличение микроскопа

Увеличение телескопа

Разрешающая способность
 , где
, где 
 , где
, где 
Закон отражения и преломления света
Преломление света
Измерения показали, что скорость света в веществе υ всегда меньше скорости света в вакууме c.
- Отношение скорости света в вакууме c к ее скорости в данной среде υ называется абсолютным показателем преломления:

Словосочетание «абсолютный показатель преломления среды» часто заменяют «показатель преломления среды».
Рассмотрим луч, падающий на плоскую границу раздела двух прозрачных сред с показателями преломления n1 и n2 под некоторым углом α (рис. 2).


Рис. 2 - Изменение направления распространения луча света при прохождении через границу раздела двух сред называется преломлением света.
Законы преломления:
- отношение синуса угла падения α к синусу угла преломления γ есть величина постоянная для двух данных сред

- лучи, падающий и преломленный, лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред.
Для преломления выполняется принцип обратимости световых лучей:
- луч света, распространяющийся по пути преломленного луча, преломившись в точке O на границе раздела сред, распространяется дальше по пути падающего луча.
Из закона преломления следует, что если вторая среда оптически более плотная через первая среда,
- т.е. n2 > n1, то α > γ
 (рис. 3, а);
(рис. 3, а); - если n2 < n1, то α < γ (рис. 3, б).

а 
б
Рис. 3 Первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшего в свет во II веке нашей эры. Закон преломления света был экспериментально установлен в 1620 г. голландским ученым Виллебродом Снеллиусом. Заметим, что независимо от Снеллиуса закон преломления был также открыт Рене Декартом.Закон преломления света позволяет рассчитывать ход лучей в различных оптических системах.
На границе раздела двух прозрачных сред обычно одновременно с преломлением наблюдается отражение волн. Согласно закону сохранения энергии сумма энергий отраженной Wo и преломленной Wnp волн равна энергии падающей волны Wn:
Wn = Wnp + Wo.
Измерения показали, что скорость света в веществе υ всегда меньше скорости света в вакууме c.
- Отношение скорости света в вакууме c к ее скорости в данной среде υ называется абсолютным показателем преломления:

Словосочетание «абсолютный показатель преломления среды» часто заменяют «показатель преломления среды».
Рассмотрим луч, падающий на плоскую границу раздела двух прозрачных сред с показателями преломления n1 и n2 под некоторым углом α (рис. 2).

- Изменение направления распространения луча света при прохождении через границу раздела двух сред называется преломлением света.
Законы преломления:
- отношение синуса угла падения α к синусу угла преломления γ есть величина постоянная для двух данных сред

- лучи, падающий и преломленный, лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред.
Для преломления выполняется принцип обратимости световых лучей:
- луч света, распространяющийся по пути преломленного луча, преломившись в точке O на границе раздела сред, распространяется дальше по пути падающего луча.
Из закона преломления следует, что если вторая среда оптически более плотная через первая среда,
- т.е. n2 > n1, то α > γ
 (рис. 3, а);
(рис. 3, а); - если n2 < n1, то α < γ (рис. 3, б).

а 
б
Закон преломления света позволяет рассчитывать ход лучей в различных оптических системах.
На границе раздела двух прозрачных сред обычно одновременно с преломлением наблюдается отражение волн. Согласно закону сохранения энергии сумма энергий отраженной Wo и преломленной Wnp волн равна энергии падающей волны Wn:
Полное отражение
Как уже говорилось выше, при переходе света из оптически более плотной среды в оптически менее плотную среду (n1 > n2), угол преломления γ становится больше угла падения α (см. рис. 3, б).
По мере увеличения угла падения α (рис. 4), при некотором его значении α3, угол преломления станет γ = 90°, т. е. свет не будет попадать во вторую среду. При углах больших α3 свет будет только отражаться. Энергия преломленной волны Wnp при этом станет равной нулю, а энергия отраженной волны будет равна энергии падающей: Wn = Wo. Следовательно, начиная с этого угла падения α3 (в дальнейшем будет обозначать его α0), вся световая энергия отражается от границы раздела этих сред.


Рис. 4 Это явление получило название полное отражение (см. рис. 4).
- Угол α0, при котором начинается полное отражение, называется предельным углом полного отражения.
Значение угла α0 определяется из закона преломления при условии, что угол преломления γ = 90°:

Как уже говорилось выше, при переходе света из оптически более плотной среды в оптически менее плотную среду (n1 > n2), угол преломления γ становится больше угла падения α (см. рис. 3, б).
По мере увеличения угла падения α (рис. 4), при некотором его значении α3, угол преломления станет γ = 90°, т. е. свет не будет попадать во вторую среду. При углах больших α3 свет будет только отражаться. Энергия преломленной волны Wnp при этом станет равной нулю, а энергия отраженной волны будет равна энергии падающей: Wn = Wo. Следовательно, начиная с этого угла падения α3 (в дальнейшем будет обозначать его α0), вся световая энергия отражается от границы раздела этих сред.

Это явление получило название полное отражение (см. рис. 4).
- Угол α0, при котором начинается полное отражение, называется предельным углом полного отражения.
Значение угла α0 определяется из закона преломления при условии, что угол преломления γ = 90°:

Правила построения изображения в линзах
Построение изображений в линзах
Световые лучи, идущие вблизи главной оптической оси. называют параксиальными (приосевыми). Мы будем рассматривать только такие лучи.
Опыт показывает, что параксиальные лучи света, выходящие из одной светящейся точки, после прохождения через линзу сходятся также в одной точке, которая являетсяизображением светящейся точки. Поэтому для построения изображения точки достаточно взять два любых луча, но лучше те, ход которых после преломления заранее известен: 1 — луч, идущий через оптический центр; 2 — луч, параллельный главной оптической оси; 3 — луч, проходящий через передний фокус собирающей линзы (или продолжение луча 3 проходит через задний фокус рассеивающей линзы) (рис. 16.41).


Рис. 16.41 Положение изображения действительного предмета и его размеры зависят от положения предмета относительно линзы. Пусть d — расстояние от предмета до линзы, f — расстояние от линзы до изображения. Построим изображение плоского предмета АВ, расположенного на различных расстояниях d от линзы.
Если линза собирающая, то при d>2F (рис. 16.42) изображение действительное, перевернутое, уменьшенное, F < f< 2F.


Рис. 16.42 При F < d < 2F (рис. 16.43) изображение действительное, перевернутое, увеличенное, f>2F.


Рис. 16.43 При d<F (рис. 16.44) изображение мнимое, прямое, увеличенное, находится с той же стороны от линзы, что и сам предмет, но дальше предмета (f>d).


Рис. 16.44 В рассеивающей линзе (рис. 16.45) изображение действительного предмета всегда мнимое, прямое, уменьшенное, находится между линзой и ее фокусом со стороны изображаемого предмета.


Рис. 16.45 Построение изображения точечного источника света расположенного на главной оптической оси, показано на рисунке 16.46.


Рис. 16.46 Чтобы найти, где образуется его изображение S1, проведем из точки S два луча: луч SO вдоль главной оптической оси (он проходит через оптический центр линзы, не преломляясь) и луч SB, падающий на линзу в произвольной точке В. Проведем побочную оптическую ось, параллельную лучу SB (показана штриховой линией). Начертим заднюю фокальную плоскость в случае собирающей линзы (переднюю фокальную плоскость в случае рассеивающей линзы). Побочная ось пересечет фокальную плоскость в побочном фокусе F’. Через этот побочный фокус пройдут все параллельные данной оптической оси лучи после преломления в собирающей линзе (или продолжения преломленных лучей в рассеивающей линзе), следовательно, и луч SB. Преломленный луч (или его продолжение) пересечет главную оптическую ось в точке S1 которая и является изображением точечного предмета S.
Информация взята с сайта ru.wikipedia.org
Световые лучи, идущие вблизи главной оптической оси. называют параксиальными (приосевыми). Мы будем рассматривать только такие лучи.
Опыт показывает, что параксиальные лучи света, выходящие из одной светящейся точки, после прохождения через линзу сходятся также в одной точке, которая являетсяизображением светящейся точки. Поэтому для построения изображения точки достаточно взять два любых луча, но лучше те, ход которых после преломления заранее известен: 1 — луч, идущий через оптический центр; 2 — луч, параллельный главной оптической оси; 3 — луч, проходящий через передний фокус собирающей линзы (или продолжение луча 3 проходит через задний фокус рассеивающей линзы) (рис. 16.41).

Положение изображения действительного предмета и его размеры зависят от положения предмета относительно линзы. Пусть d — расстояние от предмета до линзы, f — расстояние от линзы до изображения. Построим изображение плоского предмета АВ, расположенного на различных расстояниях d от линзы.
Если линза собирающая, то при d>2F (рис. 16.42) изображение действительное, перевернутое, уменьшенное, F < f< 2F.

При F < d < 2F (рис. 16.43) изображение действительное, перевернутое, увеличенное, f>2F.

При d<F (рис. 16.44) изображение мнимое, прямое, увеличенное, находится с той же стороны от линзы, что и сам предмет, но дальше предмета (f>d).

В рассеивающей линзе (рис. 16.45) изображение действительного предмета всегда мнимое, прямое, уменьшенное, находится между линзой и ее фокусом со стороны изображаемого предмета.

Построение изображения точечного источника света расположенного на главной оптической оси, показано на рисунке 16.46.

Чтобы найти, где образуется его изображение S1, проведем из точки S два луча: луч SO вдоль главной оптической оси (он проходит через оптический центр линзы, не преломляясь) и луч SB, падающий на линзу в произвольной точке В. Проведем побочную оптическую ось, параллельную лучу SB (показана штриховой линией). Начертим заднюю фокальную плоскость в случае собирающей линзы (переднюю фокальную плоскость в случае рассеивающей линзы). Побочная ось пересечет фокальную плоскость в побочном фокусе F’. Через этот побочный фокус пройдут все параллельные данной оптической оси лучи после преломления в собирающей линзе (или продолжения преломленных лучей в рассеивающей линзе), следовательно, и луч SB. Преломленный луч (или его продолжение) пересечет главную оптическую ось в точке S1 которая и является изображением точечного предмета S.
Информация взята с сайта ru.wikipedia.org